数值计算方法
计算方法
绝对误差,相对误差,与有效数字
绝对误差与相对误差
若 \(x^{*}\) 为 \(x\) 的一个近似值,则称 \(x-x^{*}\)为进似值\(x^{x}\) 的绝对误差,用 \(e^{x}(x)\) 表示
绝对误差限\(ε = x - a\)可以清楚地表明近似值与准确值之间的差异
相对误差 $e_{x}(x)= = $
有效数字的计算
若近似值\(x^{*}\)的某位数的半个单位是他的误差限,而且从该位数字到\(x^{*}\)最左边的非零数字共有N位,则这N位数字称为有效数字
半个单位的含义:以刻度尺为例子,它的最小刻度是1mm,度数我们只能确认到测量实际有没有过或者达到一个单位的一半,比如我们度数为15mm,那么其实际尺寸最小为14.5mm,最大尺寸为15.5mm,即最大误差不超过0.5mm,就是1mm的半个单位。如果以四舍五入为例的话,一个数字是14.56是保留两位有效数字的结果,那么真实数字肯定大于等于14.555小于14.565的,其误差最大为0.005,即其是0.01这个单位的一半。
计算位数时,是从该位数字到\(x^{*}\)最左边的非零数字,注意包括该位数字
非线性方程求根
非线性方程的解与二分法
问题形象:f()=0
- 如\(sinx\)=0
其中\(f(x)\)是一元函数,且\(f(x)\in C[a,b]\)问题等价于求函数\(f(x)\)的零点
重根:若\(f(x)=\left(x-x^{*}\right)^{m} g(x), g\left(x^{*}\right) \neq 0\) 则\(x^{*}\)是\(f(x)=0\)的m重根。
- 如\((x-1)^{2}\),有重根
零点定理:设函数 \(f(x)\)在闭区间[a,b],且\(f(a).f(b)<0\),则在开区间(a,b)内至少有一点 \(\xi\),使\(f(\xi)=0.\)
- 零点定理是二分法的基础
- 二分法解决问题的前提是:存在异号区间
当异号区间足够小,就可以获得足够精度的近似解。
二分法
- 思想与二分搜素中的实数二分十分相似
二分法:(前提是有异号区间,思想是不断缩小异号区间) 步骤1 计算异号区间 [a, b] 端点处的函数值 $f(a), f(b) $ ; (1) $ x_{k+1}=x_{k}^{2}+x_{k}-3 $
步骤2 计算异号区间 [a, b] 中点处的函数值 \(f\left(\frac{a+b}{2}\right)\) ;
步㵵3 若 $f()=0 $,则 $x= $是根,计算结束;
否则缩小区间: 若 $ f() f(a)<0 $ ,赋值 $ b= , f(b)=f() $ ;
若 $ f() f(b)<0 $ ,赋值 $ a= ,$ $ f(a)=f() $
转步骤2
迭代法
拉格朗日插值多项式
拉格朗日插值基函数
根据表中数据,构造拉格朗日插值基函数
| xi | 1 | 2 | 3 |
|---|---|---|---|
| yi | 1 | 0 | 0 |
$ 得 \[ l_{0}(x)=\frac{1}{2}(x-2)(x-3) \]
| xi | 1 | 2 | 3 |
|---|---|---|---|
| yi | 0 | 1 | 0 |
$ 得 \[ l_{1}(x)=-(x-1)(x-3) \]
| xi | 1 | 2 | 3 |
|---|---|---|---|
| yi | 0 | 0 | 1 |
$ 得 \[ l_{0}(x)=\frac{1}{2}(x-1)(x-2) \] ### 拉格朗日插值多项式
| xi | 1 | 2 | 3 |
|---|---|---|---|
| yi | 5 | 9 | 6 |
\(\begin{array}{l} P(x)=5 {l_{0}(x)}+9 l_{1}(x)+6 l_{2}(x) \\ P(x)=5 {l_{0}(1)}(=5)+9 l_{1}(1)(=0)+6 l_{2}(1)(=0)=5 \\ \end{array}\)
牛顿均差与牛顿插值多项式构造
牛顿均差与均差表
\(\begin{array}{l} 一阶均差:f\left[x_{0}, x_{1}\right]=\frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}} \\ 二阶均差:f\left[x_{0}, x_{1}, x_{2}\right]=\frac{f\left[x_{1}, x_{2}\right]-f\left[x_{0}, x_{1}\right]}{x_{2}-x_{0}} \end{array}\)
- 一阶均差可以看作是图像上两点连线的斜率
- 可以使用均差表计算均差
| xi | yi | 一阶均差 | 二阶均差 |
|---|---|---|---|
| 1 | \(f(1)=5\) | ||
| 2 | \(f(2)=9\) | \(f[1,2]=\frac{9-5}{2-1}=4\) | |
| 3 | \(f(3)=6\) | \(f[2,3]=\frac{6-9}{3-2}=-3\) | \(f[1,2.3]=\frac{-3-4}{3-1}=-\frac{7}{2}\) |
牛顿插值多项式构造
- 利用均差表的数据进行构造
- 用到了均差表对角线上的几个数 $ p(x)=f(1)+f[1,2] (x-1)+f1,2,3(x-2) \ p(x)=5+ 4(x-1)+-(x-1)(x-2) $
数值导数
数值导数基本问题
通过可微函数\(y=f(x)\)在某点处的函数值如\(f(x_0),f(x_1),f(x_2)\),近似计算在某点的导数值\(f'(x_1)\)
通过已知点的函数值,构造插值多项式\(P(x)\),用\(p'(x1)\)近似\(f'(x1)\)

数值积分公式的构造
数值积分公式的形象
\(\int_{a}^{b} f(x) d x \approx \sum_{k=0}^{n} A_{k} f\left(x_{k}\right)\\\)
- 根据数值积分公式,可以通过求特定点函数值,乘上特定系数,再进行组合的方式求得积分
- 注意符号使用的是约等于,但并不等于任何情况下都不等于原函数,有些情况下约等于会变成严格等于
\(\text { 例如: } \int_{a}^{b} f(x) d x \approx(b-a) f\left(\frac{a+b}{2}\right)\) 称为中矩形公式
\(\int_{a}^{b} f(x) d x \approx \frac{(b-a)}{2} f(a)+\frac{(b-a)}{2} f(b)\) 称为梯形公式
代数精度
如果某个求积公式对于次数不超过m的多项式均能准确成立,但对于m+1次 多项式就不能准确成立,则称该求积公式具有m次代数精度。 * 对于中矩形公式,当$f(x)=1,f(x)=x $时,左右两边严格相等,即中矩形公式代数精度为1
用待定系数法构造数值积分公式
确定 \(\int_{0}^{1} f(x) d x \approx A_{0} f(0)+A_{1} f\left(\frac{1}{2}\right)+A_{2} f(1)\) 的求积系数,使其代数精度尽可能高
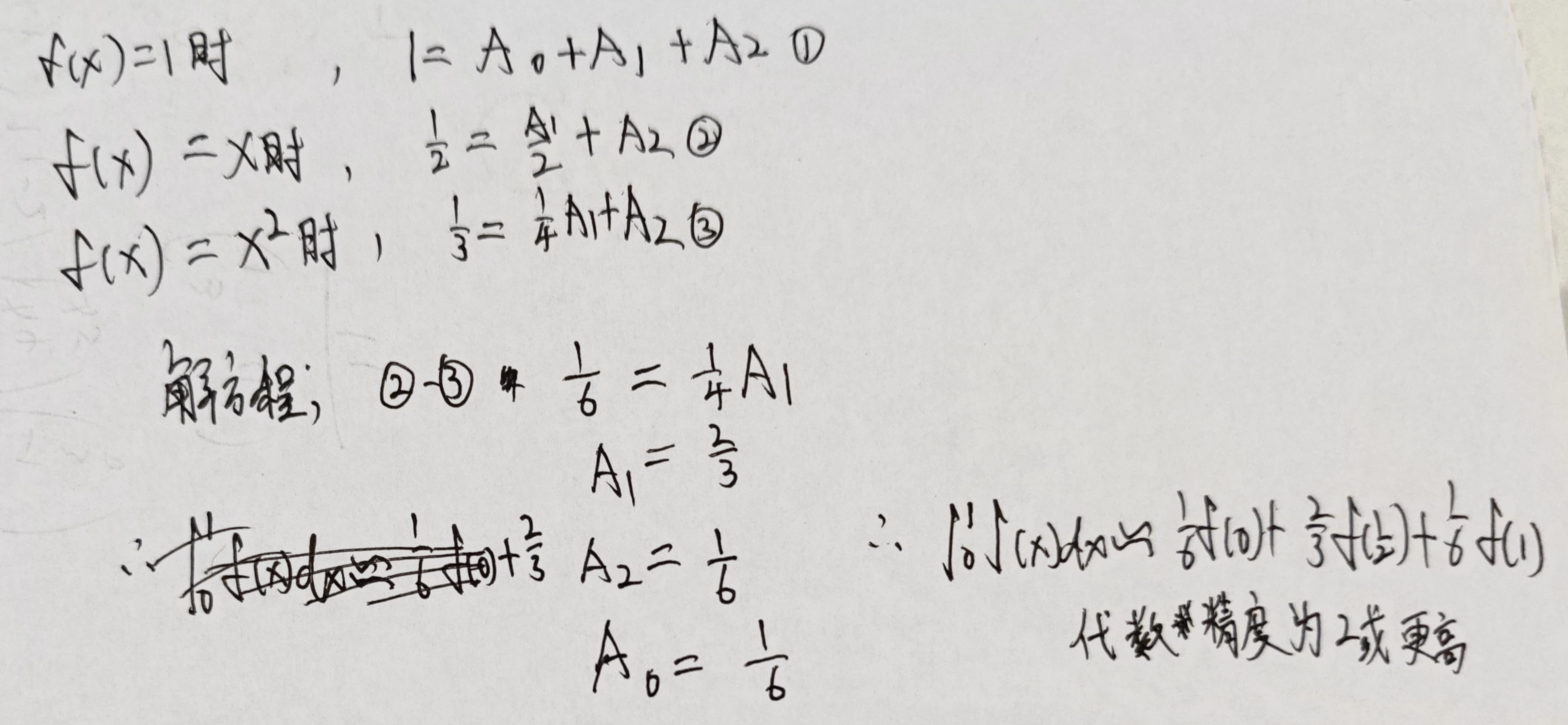 ##
矩阵的直接三角分解法解线性方程组
##
矩阵的直接三角分解法解线性方程组
矩阵的直接三角分解
\[ A=LU\]
其中,A为方阵,L为单位下三角阵,U为上三角阵。 * 注意L为单位下三角阵,即对角线都为一 * U对角线下方都为0,对角线不变 \(L=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0 \\ I_{21} & 1 & \ddots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ I_{n 1} & I_{n 2} & \cdots & 1 \end{array}\right], \quad U=\left[\begin{array}{cccc} u_{11} & u_{12} & \cdots & u_{1 n} \\ 0 & u_{22} & \ddots & u_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & u_{n n} \end{array}\right] \\\)
- 将矩阵${} $进行直接三角分解
\(A=\left[\begin{array}{ccc}
2 & 1 & 3 \\
4 & 4 & 9 \\
6 & 5 & 19
\end{array}\right] \rightarrow\left[\begin{array}{ccc}
2 & 1 & 3 \\
2 & 4 & 9 \\
3 & 5 & 19
\end{array}\right] \rightarrow\left[\begin{array}{lll}
2 & 1 & 3 \\
2 & 2 & 3 \\
3 & 1 & 19
\end{array}\right] \rightarrow\left[\begin{array}{lll}
2 & 1 & 3 \\
2 & 2 & 3 \\
3 & 1 & 7
\end{array}\right]\) 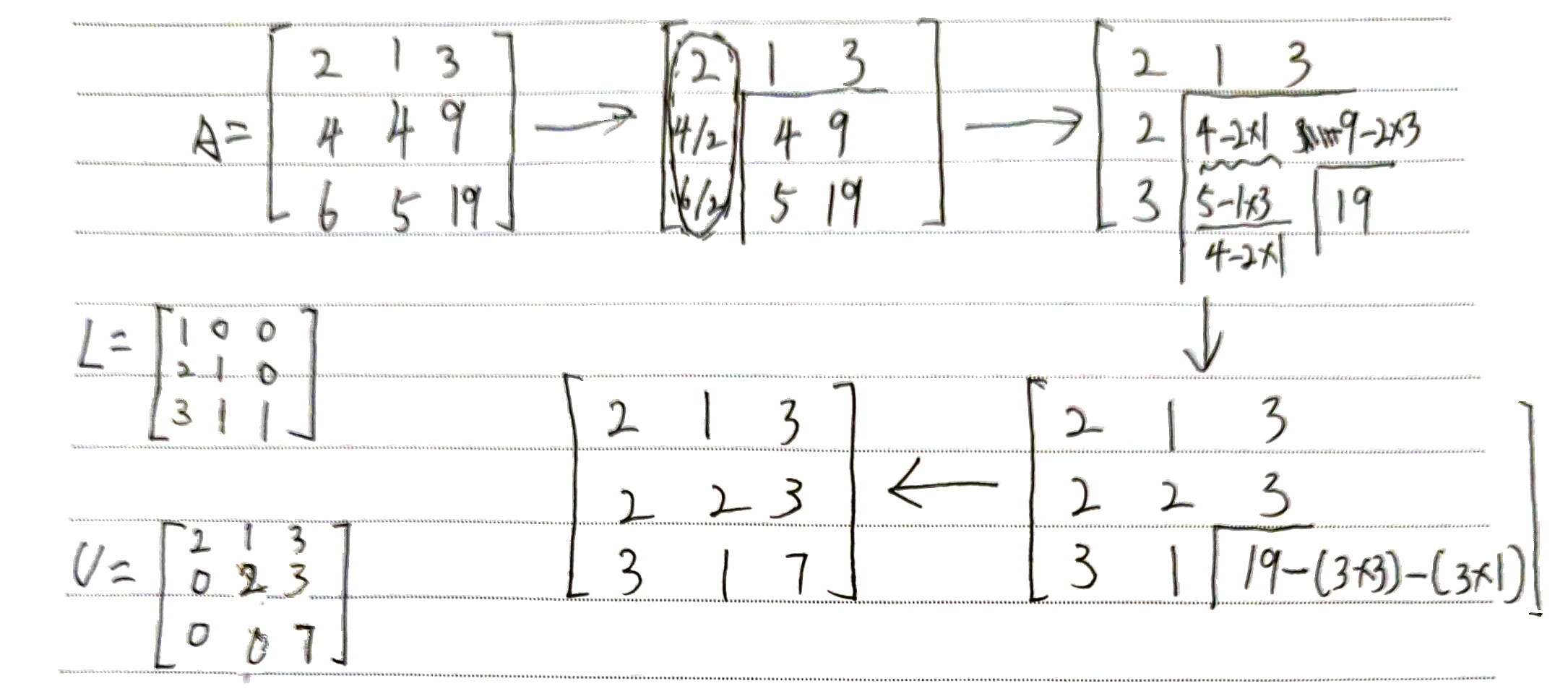 ###
利用直接三角分解解方程组
###
利用直接三角分解解方程组
如果线性方程组\(Ax=b\)的系数矩阵可以三角分解,则问题转化为 \[LUx=b\]
通过解两轮简单线性方程组 ,\(Ly=b\) ,\(Ux=y\)即可求得解。
例:求解\(\left[\begin{array}{ccc} 2 & 1 & 3 \\ 4 & 4 & 9 \\ 6 & 5 & 19 \end{array}\right]\left(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)=\left(\begin{array}{l} 3 \\ 8 \\ 11 \end{array}\right)\\\)
